専門性について
素数が出てくる規則性はあるのか? これはアメリカのクレイ数学研究所が出しているミレニアム懸賞問題の一つである「リーマンの予想」です。このリーマン予想を解くには、リーマン・ゼータ関数の自明でない零点の間隔の分布が分かれば解けることになりますが、未だ解明されていません。
一方、原子核のエネルギー準位モデルであるランダム行列理論(RMT)の式が、この分布を解く鍵となる公式と酷似していることが知られています。つまり、リーマン・ゼータ関数の零点の正規化された間隔は、ランダム行列理論を使った重い原子核のエネルギー準位の間隔と同様に、対相関関数として次式で表されます。
モンゴメリー・オドリズコ予想
いったい何のこと? 難しい話はここまでにして、要するに何が言いたいかと言いうと、素数という純粋数学と原子核のエネルギー準位という全く異なる分野の事象が実はつながっているのかも知れない,,, もし、これが証明されれば数の世界が森羅万象と関係があるという壮大な話に発展していきます。
そうなると、私は数学者、私は物理学者というような、学問の垣根とは何なのでしょうか? 学問の専門性とは何なのでしょうか? よく、会議の場で「それ、私の専門とは異なるので答えられません」という方がいます。本当の専門性とは何なのでしょうか???
文部科学省のサイトに面白い記事がありました。(https://www.mext.go.jp/b_menu/hakusho/html/others/detail/1317573.htm)
学制百年史という記事の「一.学術の発展」を読むと、要するに、日本は明治維新でいきなり何もかもがコペルニクス的転回! 学問も例外ではなく、語学が中心だったそれまでの学問が外国からいきなり西洋のそれ以外の学問(工学、医学など)が入ってきたものですから摂取して学術的研究を展開するまでには至らなかったようです。そのため、急ピッチに近代的な科学と技術の基礎を急速に築こうとしていたアタフタぶりが伺い知れます。一事が万事このような感じだったので、結局は、「学問の礎」を築くことなく、各分野が独立して学術的研究を進める情勢となっていったようです。これが、明治二十年代頃の近代科学発展への創始時代だったようです。
ここで、与えられた学問だったので「学問の礎」が取り残されてしまった日本と5000年前からリベラルアーツを行ってきた西洋では、学問の取り組み方が異なってくるのも自明の理です。本来、学問の礎とは「哲学」につながり、例えば「ヒトは何のために生きるのか?」「ヒトはなぜ死ぬのか?」シンプルな疑問に対して、様々な角度から問いかけ、検証するする「哲学」こそが重要になるのかと思います。だから、博士号はPh.D. つまり、Philosophy of Degree となるわけです。要するに、何か課題を見つけてきて、この課題を解くための道筋をつけることができて、問題解決能力を有する人に大学は「学位」を与えるわけです。ですから、どの分野で学位をとってもPh.D.なのです。
そうなると学問の礎を解くためには、時には医学、時には倫理学、時には生物学、時には哲学、時には、時にはと色々な学問分野が包括的に必要になってくるはずです。話を戻すと、専門性とは何か? 実は、「専門」なる学問的な垣根はそれほど重要ではなく、その問題を解決するためにどの分野の学問を使えば問題が解決するかを見極めることが重要で専門性に拘って問題解決を回避することは、本当に学問と言えるのか? 甚だ疑問です。
ただ、現代は、各分野の研究が深化しているため、色々なヒトと組まないと問題が解決しないのは事実です。その意味では、Specialistは必要であり、自身も何らかの分野のSpecialistになる必要があります。そして、Specialistが何人か組んで問題解決が図られていくのかと思います。つまり「私の専門ではないので」という発言は学問が分かっているヒトは言わない言葉とか私には思えてなりません。
最後に、このように考えていくと、「理系」「文系」の垣根はなく、課題を解決するためには何が必要か、必要なものが自分に備わっていなければ、その道のSpecialistである他者と組むことで、解決すべき学術的問いを解いていくことこそが重要だと思います。
これは、決してGeneralistになれということではなく、Specialistになるための専門性と問題解決に必要な論理性と視野の広さ(Bird of View)が求められるのかと思います。要するに、理系だの文系だの、はたまた(狭義の意味での)専門性がどうのこうのなど言っていることは、実に陳腐なことなのかと私には思えてなりません。
記事:大久保 剛
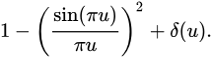
Comments